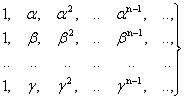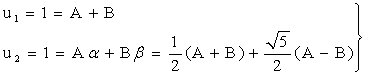де А і В повинні бути визначені з рівнянь
|
u1=A+B(1-1) |
|
|
u2=A+B(2-1) |
Звідси слідує що
|
u1=A |
|
|
u2=A+B |
Маємо
|
A=u1, B=u2-u1 |
і, отже,
|
un=u1+(n-1)(u2-u1) |
Це формула для обчислення будь-якого члена послідовності, яка задовольняє зворотне рівняння
|
un+2=2un+1—un |
Покладаючи u1=a, u2-u1=d, можна подати її у вигляді
|
un=a +(n-1)d |
Це і є відома формула для загального члена арифметичної прогресії.
Покажемо, що при деяких загальних умовах можна знайти базис зворотного рівняння.
|
un+k=a1un+k-1+a2un+k-2+…+akun, |
який складається з k геометричних прогресій з різними знаменниками. Спочатку з'ясуємо, при яких умовах деяка геометрична прогресія
|
x1=1, x2=q,…,xn=qn-1,…(q |
буде задовольняти рівняння (12). При цьому враховуючи, що
|
xn+k=qk+n-1, xn+k-1=qn+k-2, …, xn=qn-1 |
і підставляючи дані значення замість un, отримаємо
|
qk+n-1=a1qn+k-2+a2 qn+k-3+…+akqn-1 |
звідки
|
qk=a1qk-1+a2 qk-2+…+ak |
(18) |
Отже геометрична прогресія тільки тоді може задовольняти зворотне рівняння (12) порядку k, коли знаменник прогресії q задовольняє алгебраїчне рівняння (18) степеня k із тими самими коефіцієнтами, що і рівняння (12).
Рівняння (18) називається характеристичним для зворотного рівняння (12). Якщо q=α – який-небудь корінь характеристичного рівняння (дійсний чи уявний), то поклавши
|
xn=αn-1 (n=1,2,…), |
(19) |
отримаємо геометричну прогресію з першим членом x1=1 і знаменником α, яка задовольняє рівняння (12). Справді, за умовою, α є корінь рівняння (18), тобто
|
αk=a1αk-1+a2αk-2+…+αk |
Домножаючи обидві частини на αn-1, де nεN, отримаємо
|
αk+n-1=a1αn+k-2+a2αn+k-3+…+akαn-1 |
Тобто послідовність (19) задовольняє рівняння (12).
Отже, кожному кореневі q=α характеристичного рівняння (18) відповідає геометрична прогресія (19) зі знаменником α, що задовольняє зворотному рівнянню (12).
Щоб скласти базис з одних лише геометричних прогресій з різними знаменниками, потрібно мати їх у достатній кількості, рівній k, а для цього потрібно мати k різних коренів характеристичного рівняння.
Нехай, всі корені характеристичного рівняння різні
|
Q1=α, q2=β, …,qk=γ |
Тоді отримаємо k геометричних прогресій, які задовольняють рівняння (12).
|
|
(20) |
Оскільки дана система послідовностей (20) складає базис рівняння (12), можна підібрати такі числа A,B,…,C, що при довільному n.
|
un=Aα n-1+Bβn-2+…+Cγn-1 |
Як приклад застосування даних результатів розглянемо послідовність чисел Фібоначчі. Для них зворотне рівняння має вигляд
|
un+2=un+1+un |
Відповідно до рівняння (18) характеристичне рівняння має вигляд
|
q2=q+1 |
Коренем цього рівняння є два різних дійсних корені
|
|
Туму загальний член послідовності Фібоначчі можна записати так
|
un=Aαn-1+Bβn-1 |
Для того, щоб знайти невідомі коефіцієнти A і B, покладемо n=1 і n=2; отримаємо
|
|
Коренями даної системи є числа
|
|