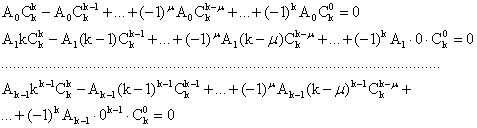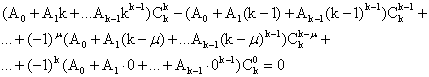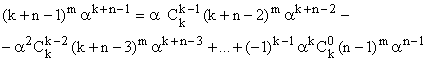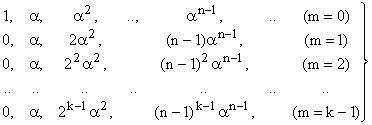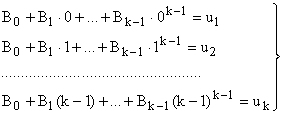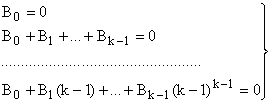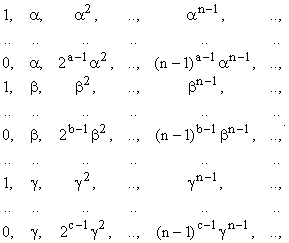Зворотні послідовності

Це і є рівність (26) для m=j+1. Таким чином доведена рівність (26).

Розглянемо, нарешті, довільний многочлен степеня не вище k-1:

Домножаючи рівність (26) при m=1,2,…,k-1 відповідно на A0, A1,…, Ak-1, отримаємо

Додаючи їх почленно, будемо мати

або

Отже, довільний многочлен P(x) степеня не вище k-1 задовольняє співвідношенню (30).

Покладемо, зокрема, Р(х)=(х+n-1)m, де n ‑ довільне натуральне число і m — ціле, 0<m≤k-1. Тоді рівність (30) набуде вигляду

Або, домножаючи на αk+n-1 і замінюючи на 1:

Порівнюючи (31) із (21), приходимо до висновку, що зворотному рівнянню (21) задовольняє кожна з k послідовностей

Якщо ми встановимо, що вони утворюють базис, то звідси. буде .випливати, що загальний член довільної послідовності, що задовольняє рівняння (21), має вигляд

де Q(x)=B0+B1x+…+Bk-1xk-1 – многочлен степеня не вище k-1 з довільними коефіцієнтами.

Достатньо показати, що система k лінійних рівнянь

має розв’язок відносно невідомих при будь-яких u1,…uk тобто в силу положень, що були запропоновані вище, система

має тільки нульовий розв’язок. Проте рівняння останньої системи означають, що

тобто, що рівняння

степеня не вище k-1 має, в крайньому випадку, k різних корені: 0,1,2,…,k-1. Звідси випливає що

Отже послідовності (32) утворюють базис зворотних послідовностей, які задовольняють рівнянню (21).

У випадку довільної зворотної послідовності, яка задовольняє загальне рівняння

характеристичне рівняння

може мати деякий корінь α кратності a, корінь β кратності b,…, корінь γ кратності c, а всього a+b+…+c=k коренів.

Для цього найбільш загального випадку можна показати, що базис складається з наступних k послідовностей

Тому

Де Q(x), R(x), ., S(x) – деякі фіксовані многочлени, степеня не вище a-1, b-1,…,c-1 відповідно.

Отже, загальний член un будь-якої зворотної послідовності має вигляд суми добутків многочленів відносно n-1 (або, що зводиться до того ж, відносно n) на загальні члени геометричних прогресій, знаменники яких дорівнюють кореням характеристичного рівняння (35).

У випадку, коли всі корені останнього рівняння— прості, зазначені многочлени є сталими і загальний член зворотної послідовності подається у виді суми членів геометричних прогресій.

Можна довести також справедливість оберненого твердження. А саме, будь-яка послідовність {un}, загальний член якої виражається за формулою, (36), є зворотною. Відповідне характеристичне рівняння (35) будується за його коренях α,β, .,γ і за їх крайностях a,b,…,c (які являють собою степені многочленів Q,R, ,S, збільшені на одиницю). Звідси негайно знаходиться зворотне рівняння (34).

Розглянемо у виді прикладу послідовність.

Порівнюючи з (36), доходимо висновку, що корені характеристичного рівняння такі: α=2, β=3, причому кратність α дорівнює 2+1=3. Тому характеристичне рівняння повинно мати вигляд

а зворотне рівняння запишеться так;