2) z = -2+2Ö3ί;
Маємо: tg α = 2Ö3/(-2) = -3. Тут а = -2, b = 2Ö3, тобто радіус – вектор, який відповідає даному комплексному числу, належить ІІ чверті. Отже, α = π 2/3.
3) z = -1-ί;
Маємо: tg α = 1. Радіус – вектор, що відровідає даному комплексному числу, належить ІІІ чверті. Отже, α = π 5/4.
4) z = 1-Ö3ί;
Маємо: tg α = -Ö3. Тут а = 1, b = -Ö3. Радіус – вектор, що відповідає даному комплексному числу, належить IV чверті. Отже, = π 5/3.
в) тригонометрична форма комплексного числа.
Нехай вектор ОА є геометричним зображенням комплексного числа z = a + bί (дивіться малюнок 7), модуль якого дорівнює r, а аргумент α. У прямокутному трикутнику АОС а = r cos α, d = r sin α. Підставляючи у запис комплексного числа замість а та d їхні значення, виражені через модуль і аргумент, дістанемо :
Z = r cos α + ίr sin αί = r(cos α + ίsin α).
Вираз r(cos α + sin αί) називається тригонометричною формою комплексного числа. Будь – яке число a + bί, дане в алгебраїчній формі, можна подати в тригонометричній формі. Модуль r знаходимо за формулою r =Ö a² + b², а кут α визначаємо із залежності tg α =b\a, яка випливає з формул cos α = a\r, sin α = b\r.
Приклади:
а) z = -1-Ö3ί;
Маємо: r = Ö(-1)²+(- Ö3)² = 2; tg α = Ö3; α = 4π\3 + πn, n є Z.
Через те, що радіус – вектор, який зображує число z = a + bί, розміщений у ІІІ чверті комплексної площини, то за аргумент беремо α = 4π\3 + πn. Отже, -1-Ö3ί = 2(соs 4π\3 + ί Sin 4π\3).
б) z = ί;
Тут а = 0, b = 1, отже, r = 1. Вектор, що зображує число ί, утворює з віссю абсцисс кут π\2 (поясніть чому). Отже, ί = cos π\2 + ί sin π\2.
в) z = 3.
Тут а = 3, b = 0, отже, r = 3.
3 = 3(cos 0 + ί sin 0).
Розглянемо приклади переходи від тригонометричної форми комплексного числа до алгебраїчної.
Приклади:
а) 2(cos π\3+ ί sin π\3) = 2(1\2+Ö3ί \2) = 1 +Ö3ί;
б) 4(cos 2π\3 + ί sin 2π\3) = 4(-1\2+Ö3ί \2) = -2 + 2Ö3ί.
г) Множення і ділення комплексних чисел, записаних в тригонометричній формі.
Тригонометрична форма запису комплексних чисел виявляється дуже зручною під час множення і ділення чисел. Нехай Z₁=r₁(cos α₁ + ί sin α₁), Z₂=r₂(cos α₂ + ί sin α₂) – два числа, що записані в тригонометричній формі. Тоді
Z₁ Z₂= r₁r₂( cos α₁ cos α₂ - sin α₁ sin α₂ + ί sin α₁cos α₂ + ί sin α₂ cos α₁), або Z₁ Z₂= r₁r₂( cos (α₁ + α₂) + ί sin (α₁ + α₂)). Отже, справедливим є твердження: під час множення комплексних чисел у тригонометричній формі модулі їх перемножуються, а аргументи додаються. Для знаходження частки множимо чисельник і знаменник на число, спряжене до знаменника:
Z₁\Z₂=r₁(cos α₁ + ί sin α₁)(cos α₂ - ί sin α₂)\ r₂(cos α₂ + ί sin α₂)(cos α₂ - ί sin α₂) = r₁\r₂х(cos (α₁ - α₂) + ί sin (α₁ - α₂))\( cos² α₂ + ί sin ²α₂)= r₁( cos (α₁ - α₂) + ί sin (α₁ - α₂))\r₂.
Отже, під час ділення комплексних чисел їх модулі діляться, а аргументи віднімаюьтся.
Приклади. Виконати множення і ділення комплексних чисел, записаних у тригонометричній формі.
а) Z₁=3(cos 7° + ί sin 7°); Z₂=8(cos 15° + ί sin 15°);
д) Подаємо без доведення правила піднесення до степеня комплексного числа, записаного в тригонометричній формі.
При будь – якому натуральному n
(cos α + ί sin α)ⁿ = cos nα + ί sin nα.
Це твердження називається формулою Муавра.
Приклади. Виконати дії піднесення до ступеня даного комплексного числа.
Z=Ö3-ί. Обчислити Z.
Модуль даного числа дорівнює Ö(Ö3)²+1 = 2, аргумент α = -π\6, отже модуль числа Z дорівнює 2, аргумент 9α = -9π\6 = -3π\2. Таким чином,
(Ö3-ί) = 2 (cos (-3π\2)+ ί sin(-3π\2)) = 512ί.
є) добування кореня з комплексного числа.
Корінь n – го ступеня з числа Z=r(cos α + ί sin α) обчислюють за формулою
ω = Ör(cos ((α + 2 πк)\n) + ί sin ((α + 2 πк)\n)),
де к – деяке ціле число (к є Z).
Підставляючи замість к значення 0, 1, 2…n – 1, дістанемо n різних значень кореня. Так, якщо n = 2, к = 2 матимемо sin ((α + 4 π) = sin α\2 і так далі.
Приклади. Знайти всі значення Ö1
Оскільки 1 = 1(cos 0 + ί sin 0), то
Ö1(cos 0 + ί sin 0) = 1(cos ((0 + 2 πк)\5) + ί sin ((0 + 2 πк)\5), к = 0, 1, 2, 3, 4. Надаючи к послыдовно значень 0, 1, 2, 3, 4, выдповыдно дыстанемо:
Z₁= 1, якщо к = 0;
Z₂= cos 2π\5 + ί sin 2π\5, якщо к = 1;
Z₃= cos 4π\5 + ί sin 4π\5, якщо к = 2;
Z₄= cos 6π\5 + ί sin 6π\5, якщо к = 3;
Z₅= cos 8π\5 + ί sin 8π\5, якщо к = 4.
Цікавий такий факт. Модулі всіх цих значень Ö1 дорівнюють 1. Отже, точки Z₁, Z₂, Z₃, Z₄, Z₅ лежать на колі радіуса 1 з центром у початку координат. Побудувавши аргументи значень Z₁, Z₂, Z₃, Z₄, Z₅ , помітимо, що точки, які зображують числа Z₁, Z₂, Z₃, Z₄, Z₅, є вершинами правильного п’ятикутника (малюнок 7).
Взагалі точки, які відповідають значенням кореня n – го ступеня з комплексного числа Z=r(cos α + ί sin α), розміщуються у вершинах правильного n – кутника з центром у точці О.
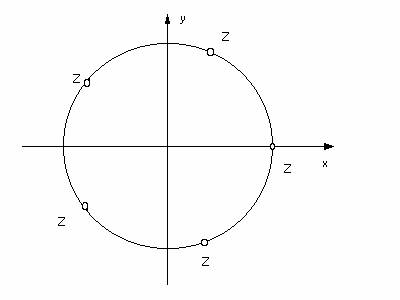Малюнок 7
Завантажити реферат